Editar

Propiedades y representaciones:

• 
  Editar

  Ángulo de oroEditar

  ${\displaystyle {\frac {360^{\circ }}{\varphi +{1}}}\approx 137{,}5^{\circ }}$razón número áureo

  Propiedades aritméticasEditar

  • ${\displaystyle \textstyle \varphi \approx 1,618033988749894848204586834365638117720309...}$es el único número real positivo tal que:

  ${\displaystyle \varphi ^{2}=\varphi +1\ }$

  • φ posee además las siguientes propiedades:

  ${\displaystyle \varphi -1={\frac {1}{\varphi }}\ }$

  ${\displaystyle \varphi ^{3}={\frac {\varphi +1}{\varphi -1}}\ }$

  • Las potencias del número áureo pueden expresarse en función de una suma de potencias de grados inferiores del mismo número, establecida una verdadera susecion recurrente de potencias.

  El caso más simple es:${\displaystyle \Phi ^{n}=\Phi ^{n-1}+\Phi ^{n-2}\,}$, cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.

  Una ecuación recurrente de orden ktiene la forma:

  ${\displaystyle a_{1}u_{n+k-1}+a_{2}u_{n+k-2}+...+a_{k}u_{n}\,}$,donde

  ${\displaystyle a_{i}\,}$es cualquier númerl real o complejo y k es un número natural menor o igual a n y mayor o igual a 1. 

   de potencias.

El caso más simple es:${\displaystyle \Phi ^{n}=\Phi ^{n-1}+\Phi ^{n-2}\,}$

 cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.

Una ecuación recurrente de orden ktiene la forma:

${\displaystyle a_{1}u_{n+k-1}+a_{2}u_{n+k-2}+...+a_{k}u_{n}\,}$, donde

${\displaystyle a_{i}\,}$es cualquier número real, k es un número natural menor o igual a n y mayor o igual a 1. 

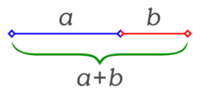
El número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b, que cumplen la siguiente relación:

✴La longitud total, suma de los dos segmentos a y b, es al segmento mayora, lo que este segmento a es al menor b. Escrito como ecuación algebraica:

${\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}}$

✴Siendo el valor del número áureo φ el cociente:${\displaystyle \phi =a/b}$

La ecuación se expresa de la siguiente manera:

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1,61803398874988...}$

El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total a+bes al segmento más largo a, comoa es al segmento más corto b.

1.